PROBLEM TRI TELA: PERIODIČNE TRAJEKTORIJE I TOPOLOŠKA KLASIFIKACIJA
Milovan Šuvakov, Veljko Dmitrašinović
Laboratory for gaseous electronics
Center for non-equilibrium processes
Institute of physics Belgrad

April 2014.
Transition Styles
You can select from different transitions, like:
Cube -
Page -
Concave -
Zoom -
Linear -
Fade -
None -
Default
Themes
Reveal.js comes with a few themes built in:
Sky -
Beige -
Simple -
Serif -
Night -
Default
* Theme demos are loaded after the presentation which leads to flicker. In production you should load your theme in the <head> using a <link>.
Saradnik Veljko Dmirtrašinovic

BAZIRANO NA RADOVIMA:


- "Numerical Search for Periodic Solutions in the Vicinity of the
Figure-Eight Orbit: Slaloming around Singularities on the Shape
Sphere", M. Suvakov, submitted to Celestial Mechanics and Dynamical
Astronomy, arXiv:1312.7002
- "A guide to hunting periodic three-body orbits", M. Suvakov and V. Dmitravsinovic, American Journal of Physics, in press
SADRŽAJ
- MOTIVACIJA: kako & zašto čestičar i plazmaš počinju da rade na problemu nebeske mehanike?
- Uvod: podsetnik - 2 tela / 3 tela
- Uvod: pregled poznatih orbita - klasične / skorašnje
- Alati: klasifikacija orbita: pletenice i sfera oblika
- Neka nova rešenja
- Zaključak, pitanja
[www.phdcomics.com]
MOTIVACIJA
- Efektivni međukvarkovski potencijali: Y i $\Delta$ struna
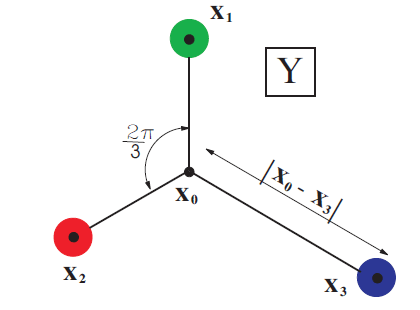
[V. Dmitrašinović, T. Sato, M. Šuvakov, Eur Phys J C 62 383 (2009)]
[V. Dmitrašinović, T. Sato, M. Šuvakov, Phys Rev D 80 054501 (2009)]
MOTIVACIJA
- Spektar ovih sistema ima određene regularnosti: Y-struna egzaktnu, $\Delta$ aproksimativnu O(2) simetriju
- Prelazak na klasičnu mehaniku
[M. Šuvakov, V. Dmitrašinović Phys Rev E 83 056603 (2011)] - Pitali smo se sledeće:
- da li postoji orbita "osmica" za Y i $\Delta$ potencijal? Da
- da li možemo naći i druge orbite za Y i $\Delta$ potencijal? Da
- da li možemo naći i druge orbite za Njutnov potencijal? Da !
UVOD: PROBLEM DVA TELA
- Dimenzija konfiguracionog prostora: 2 x 2 = 4
- Dimenzija faznog prostora: 2 x 4 = 8
- Zakoni održanja:
- energija: 1
- impuls: 2 + 2
- ugaoni momenat: 1
- Laplace-Runge-Lenz-ov vektor - 1
- Maksimalno super-integrabilni sistem (rešenja?)
UVOD: PROBLEM TRI TELA

- Dimenzija konfiguracionog prostora: 3 x 2 = 6
- Dimenzija faznog prostora: 2 x 6 = 12
- Zakoni održanja:
- energija: 1
- impuls: 2 + 2
- ugaoni momenat: 1
- H. Bruns, [Acta Math. 11, 25 (1887) ]: Nema više!
- ostalo: 6 = 3 + 3 = 3 d.o.f.
UVOD: PROBLEM TRI TELA
- Rešenja mogu biti:
- ograničena / neograničena
- periodična / kvaziperiodična / haotična
- H. Poincare:
... ono što čini ova (periodična) rešenja tako dragocenim za nas, je to da su ona, takoreći, jedini otvor kroz koji možemo da probamo da prodremo u mesto koje je, do sada, delovalo nepristupačnim.
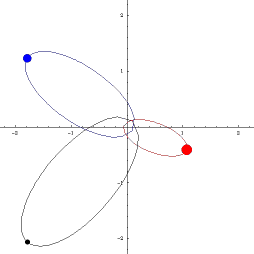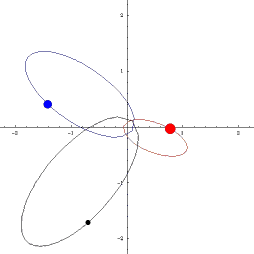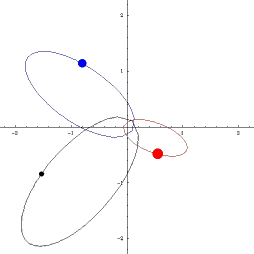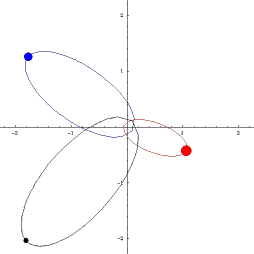
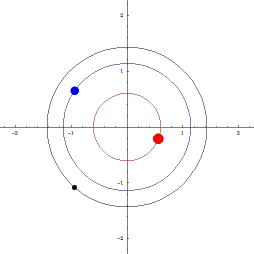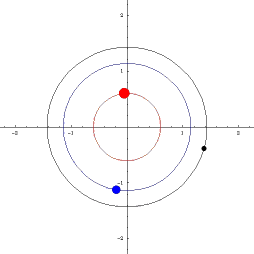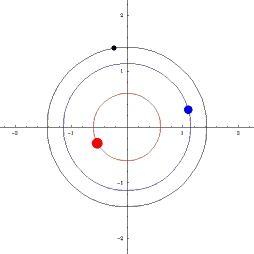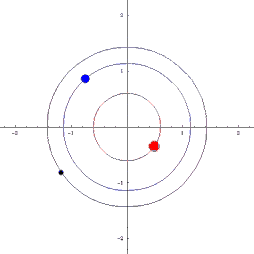
UVOD: POZNATE ORBITE TRI TELA
|
|
Klasične orbite u astronomiji:
|
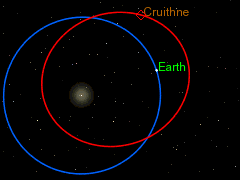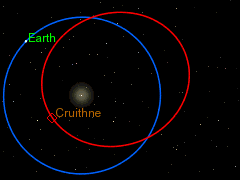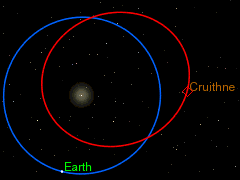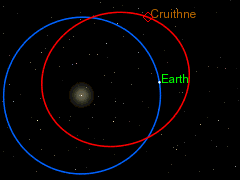 
|
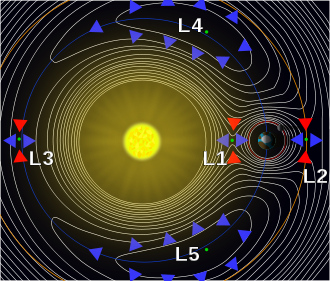
UVOD: JOŠ NOVIJE ORBITE
|
 |
MUROVA REŠENJA
|
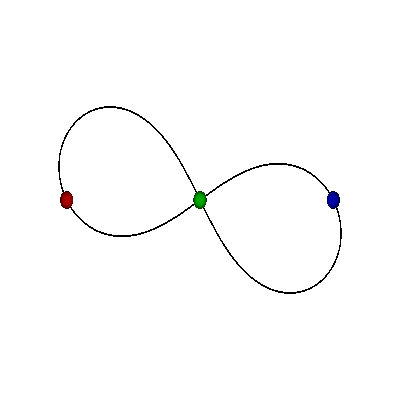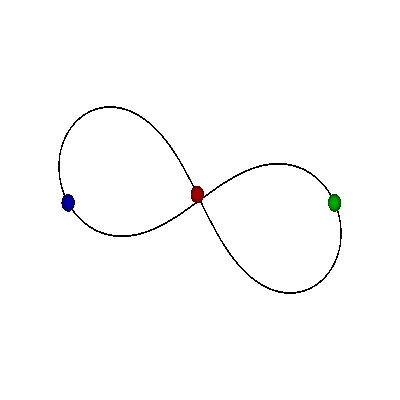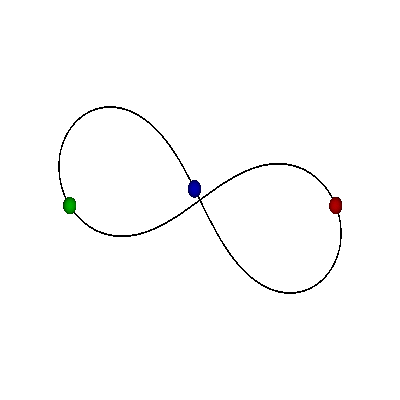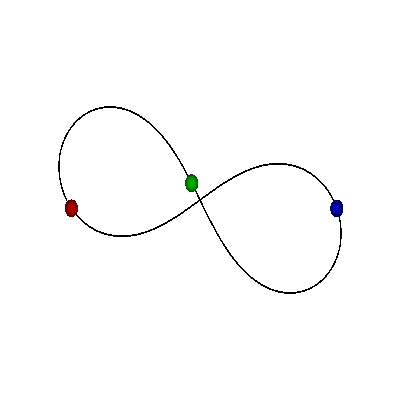
OSMICA
|
MUROVA OSMICA
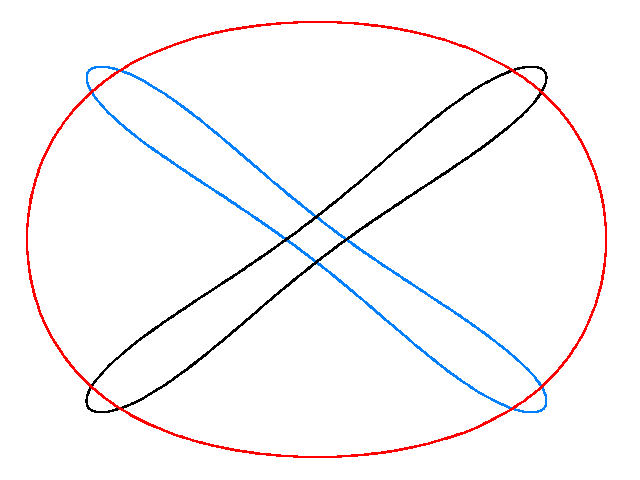
ALAT: KLASIFIKACIJA PLETENICAMA
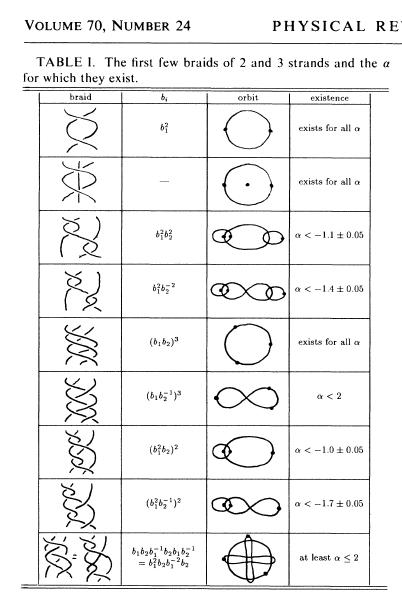
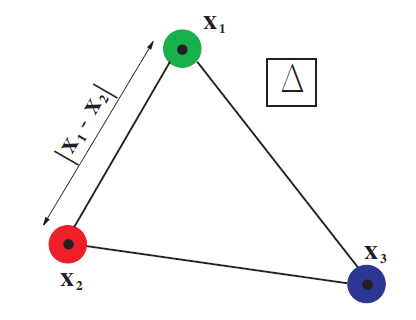
ALAT: JAKOBIJEVE KOORDINATE
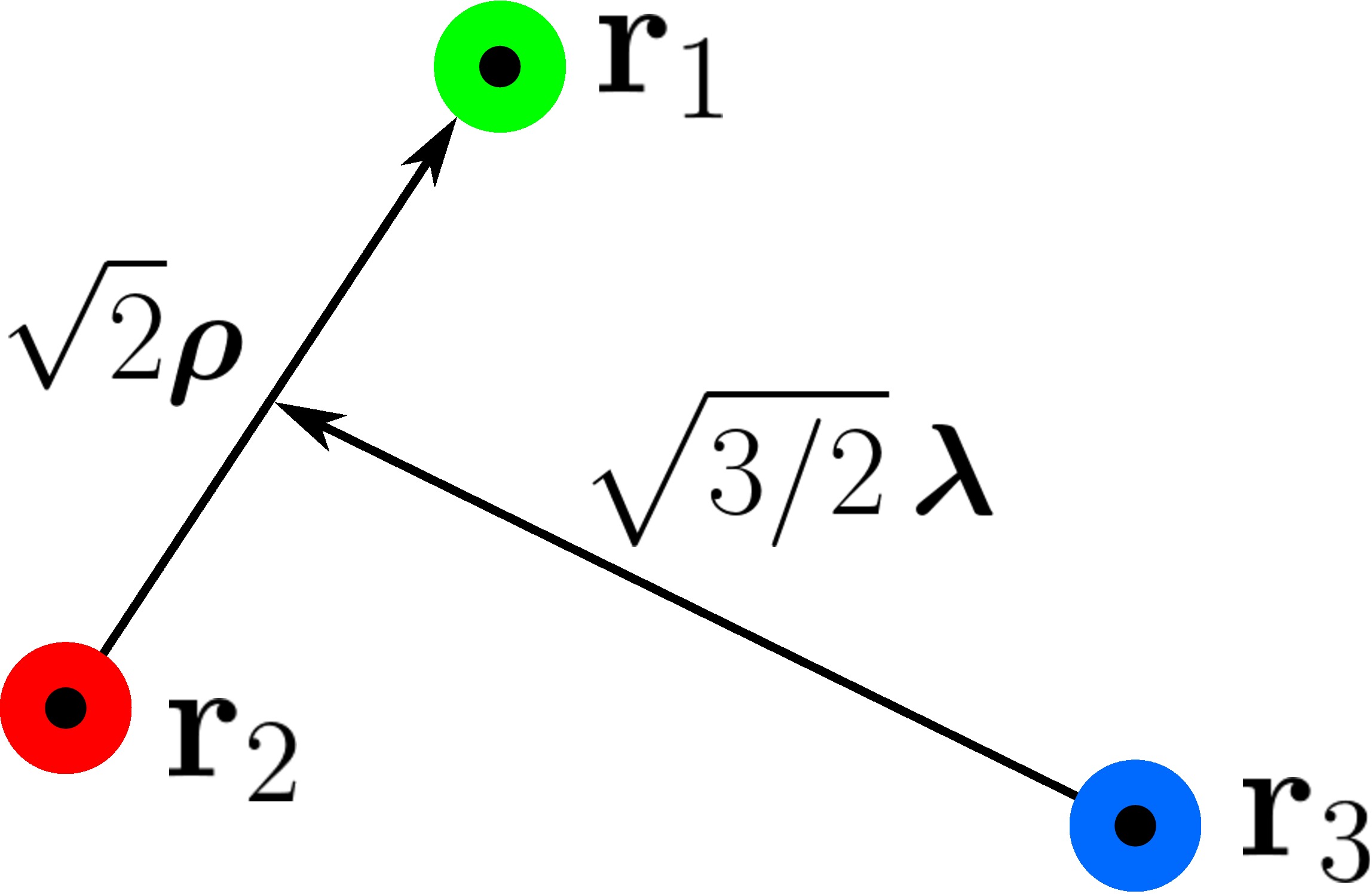 $$\rho = \frac{1}{\sqrt{2}} (\mathbf{x}_1-\mathbf{x}_2)$$
$$\lambda = \frac{1}{\sqrt{6}}
(\mathbf{x}_1+\mathbf{x}_2-2 \mathbf{x}_3)$$
Komplikovana reprezentacija permutacione simetrije!
$$\rho = \frac{1}{\sqrt{2}} (\mathbf{x}_1-\mathbf{x}_2)$$
$$\lambda = \frac{1}{\sqrt{6}}
(\mathbf{x}_1+\mathbf{x}_2-2 \mathbf{x}_3)$$
Komplikovana reprezentacija permutacione simetrije!
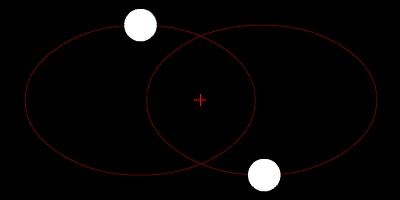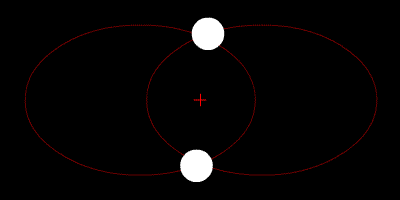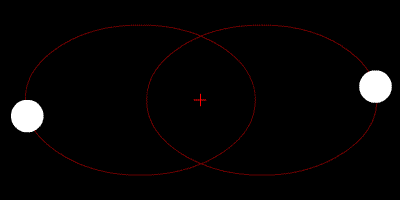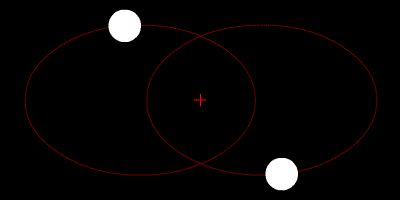
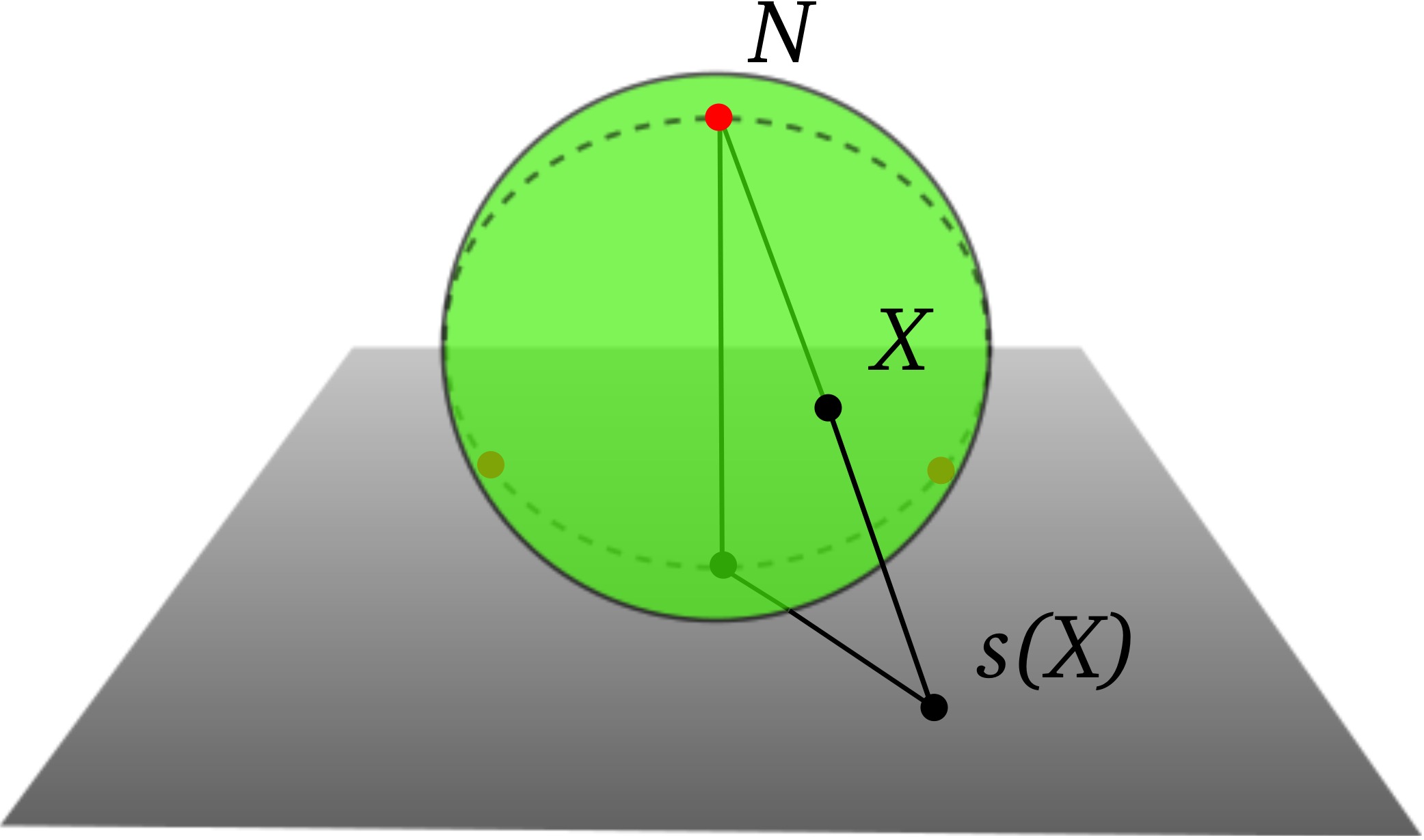
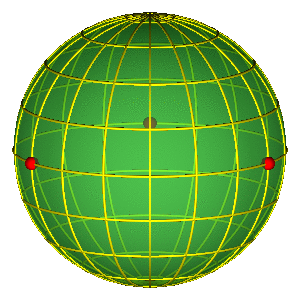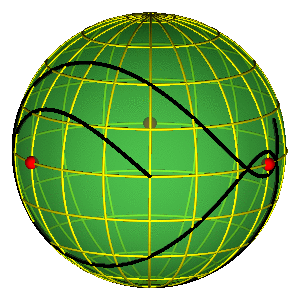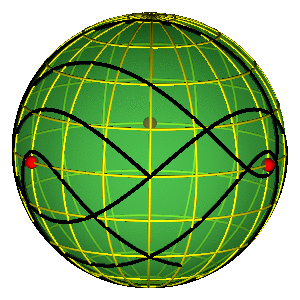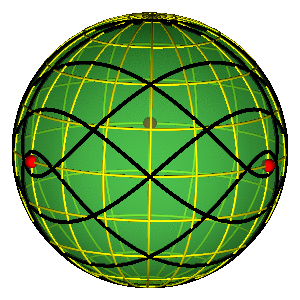
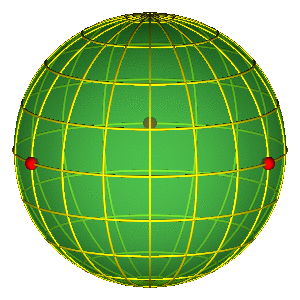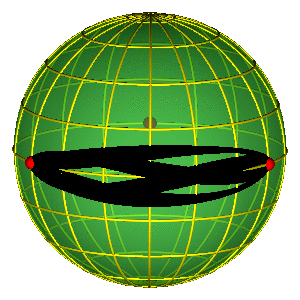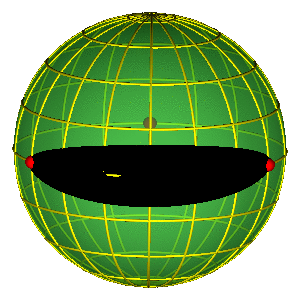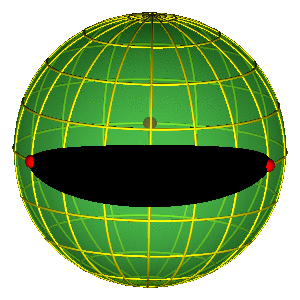
ALAT: SFERA OBLIKA
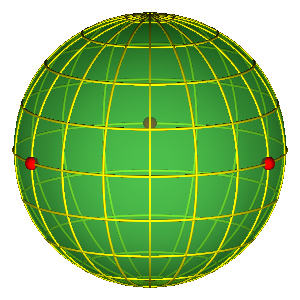 $$ \vec n = (n_x^{'},n_y^{'},n_z^{'}) = \left(\frac{2 {\vec \rho} \cdot {\vec \lambda}}{R^2}, \frac{\lambda^2 - \rho^2}{R^2}, \frac{2 ({\vec \rho} \times {\vec \lambda}) \cdot \vec e_z}{R^2} \right ) $$
$$R = \sqrt{\rho^{2} + \lambda^{2}}~~({\rm hyper-radius = ~''size''})$$
$$ \vec n = (n_x^{'},n_y^{'},n_z^{'}) = \left(\frac{2 {\vec \rho} \cdot {\vec \lambda}}{R^2}, \frac{\lambda^2 - \rho^2}{R^2}, \frac{2 ({\vec \rho} \times {\vec \lambda}) \cdot \vec e_z}{R^2} \right ) $$
$$R = \sqrt{\rho^{2} + \lambda^{2}}~~({\rm hyper-radius = ~''size''})$$
Osnovna svojstva sfere oblika
- Jednostavna reprezentacija permutacione simetrije
- Tri crvene tačke na ekvatoru predstavljaju tri binarna sudara
SFERA OBLIKA "ODOZGO"
- Hemisfere odgovaraju različitim orijentacijama (refleksija)
- Severni i južni pol su jednakostranični trouglovi (do na orijentaciju)
- Ekvator: kolinearne konfiguracije, sizigije (degenerisani trouglovi)
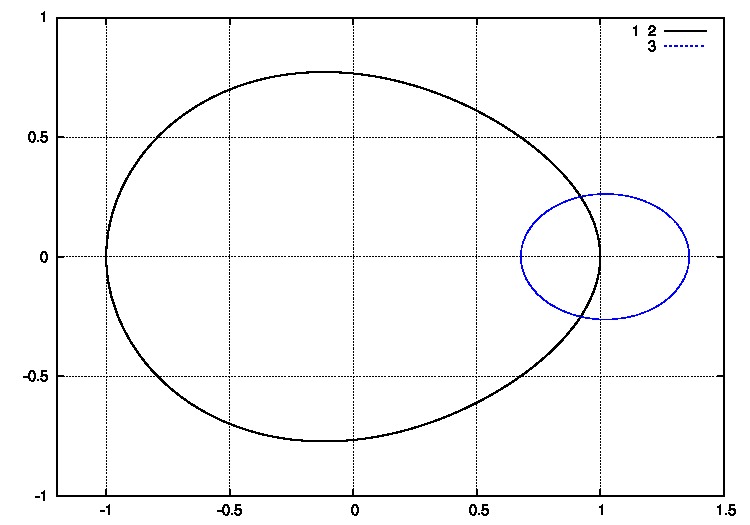
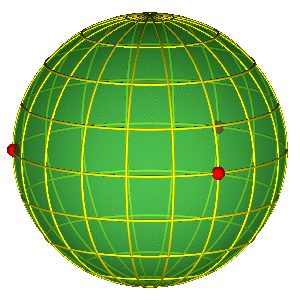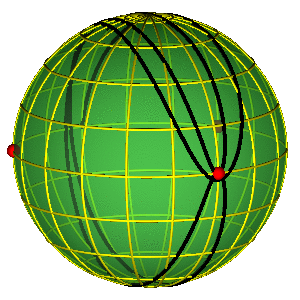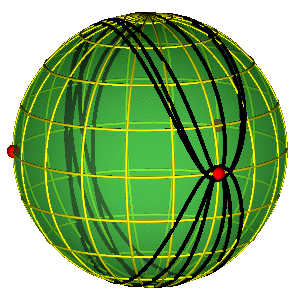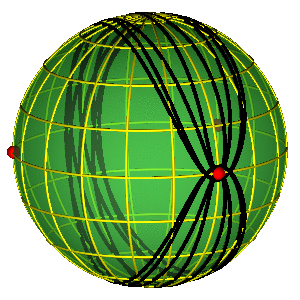
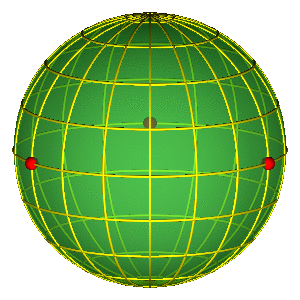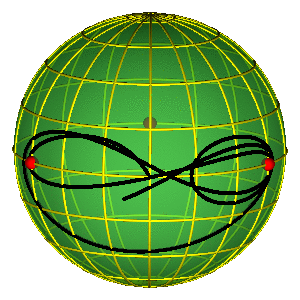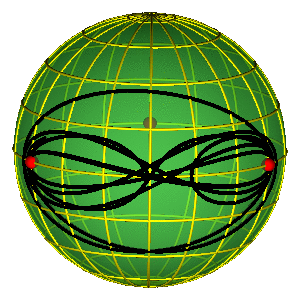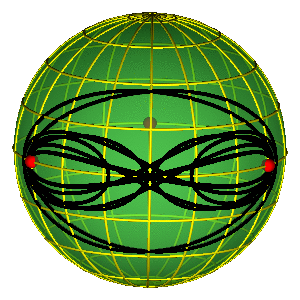
PERIODIČNE ORBITE NA SFERI OBLIKA
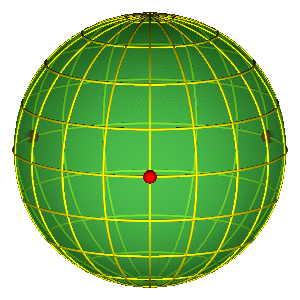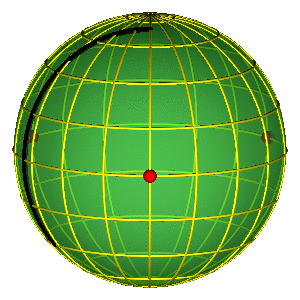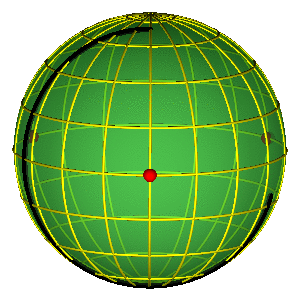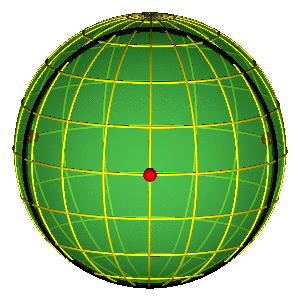
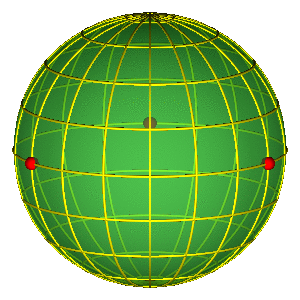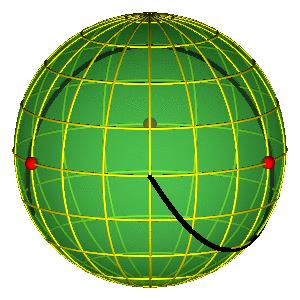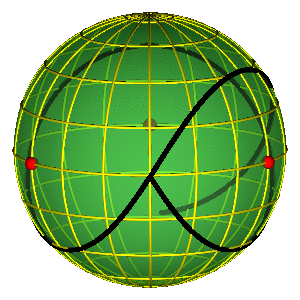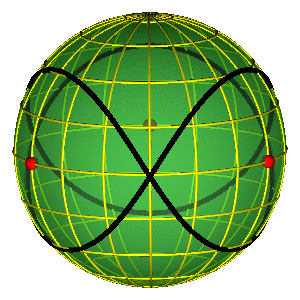
- Periodične orbite su zatvorene petlje na sferi
- Orbite bez sudara obiilaze tri sudarne tačke
- Nemoguće je kontinualno prevući orbitu preko sudarne tačke
- Primer na slici je jedna Bruk-Enonova orbita i osmica
ALAT: KLASIFIKACIJA ORBITA POMOĆU SFERE OBLIKA
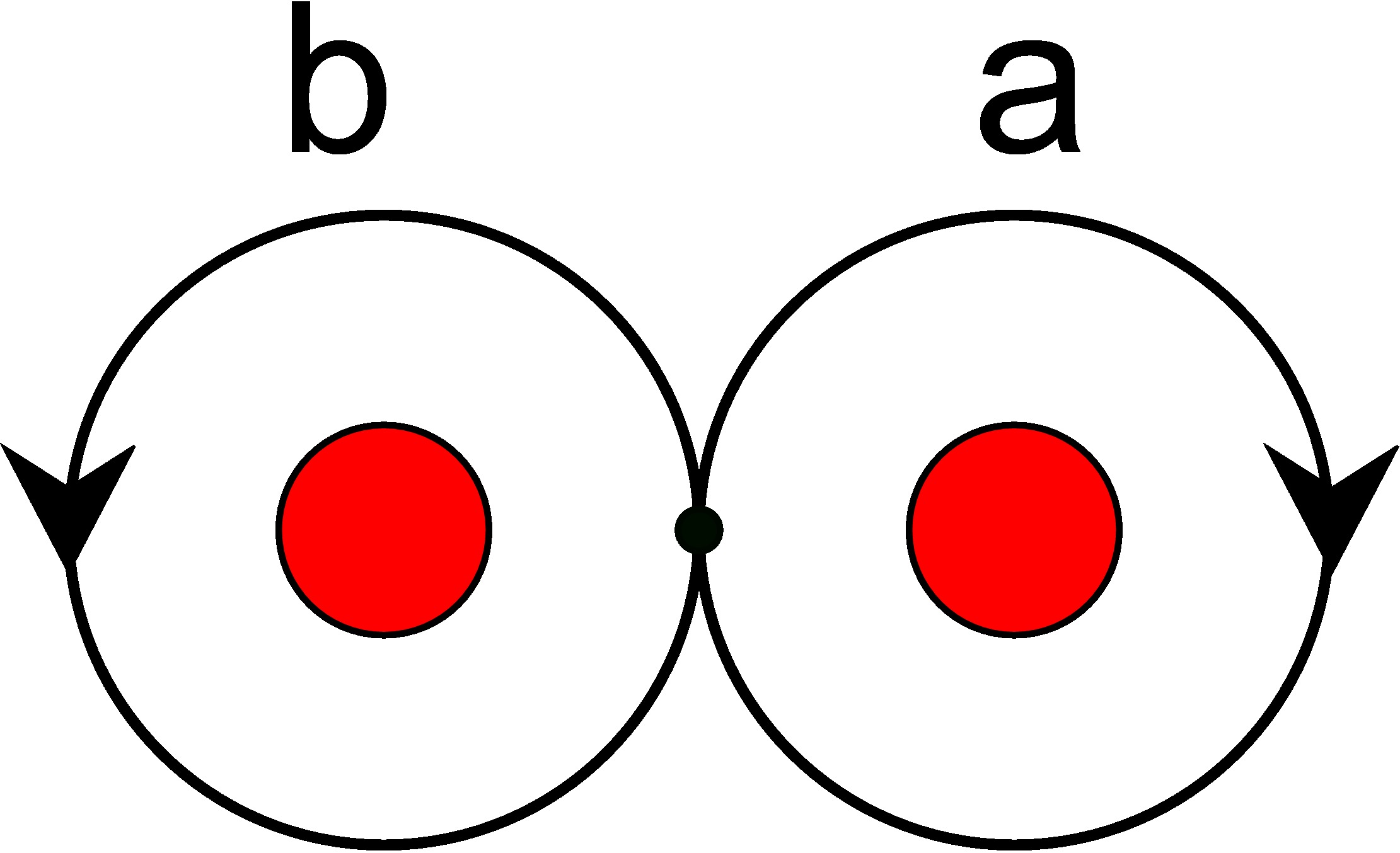
- Sfera sa tri "rupe" je homeomorfna ravni sa dve (stereografska projekcija).
- Označimo orijentisane petlje oko tih "rupa" sa dva "slova": $a,b$.
- Petlje (orbite) klasifikuju klase konjugacije slobodne grupe sa ova dva generatora.
ALAT: KLASIFIKACIJA ORBITA POMOĆU SFERE OBLIKA
- Periodične orbite su opisane klasama konjugacije slobodne grupe sa dva generatora ($a,b$).
- Zbog lakšeg zapisa koristimo velika slova za inverzne elemente: $A=a^{-1}$, $B=b^{-1}$.
- Bruk-Enon --- $a$, ili $b$ (do na permutaciju)
- Murova osmica --- $abAB$ = $(abAB, BabA, ABab, bABa)$
LOV NA NOVA REŠENJA: PRETPOSTAVKE
- Kretanje u ravni
- Jednake mase $m_{1,2,3}=1$
- Njutnova interakcija sa konstantom $G=1$ (potencijal = $-1/r$).
- Restrikcija početnih uslova na negativnu energiju i ugaoni momenat $L=0$
- Fazni prostor je 6D. Ako eliminišemo skaliranjem jedan parametar i
posmatramo sizigije, ostaje nam 4D. Dva dodatna uslova:
- $R'(0)=0$: (-1 dim.)
- Simetrična sizigija - Ojlerova konfiguracija: (-1 dim.)
- Sa ovim uslovima ostalo je dva stepena slobode.
METOD
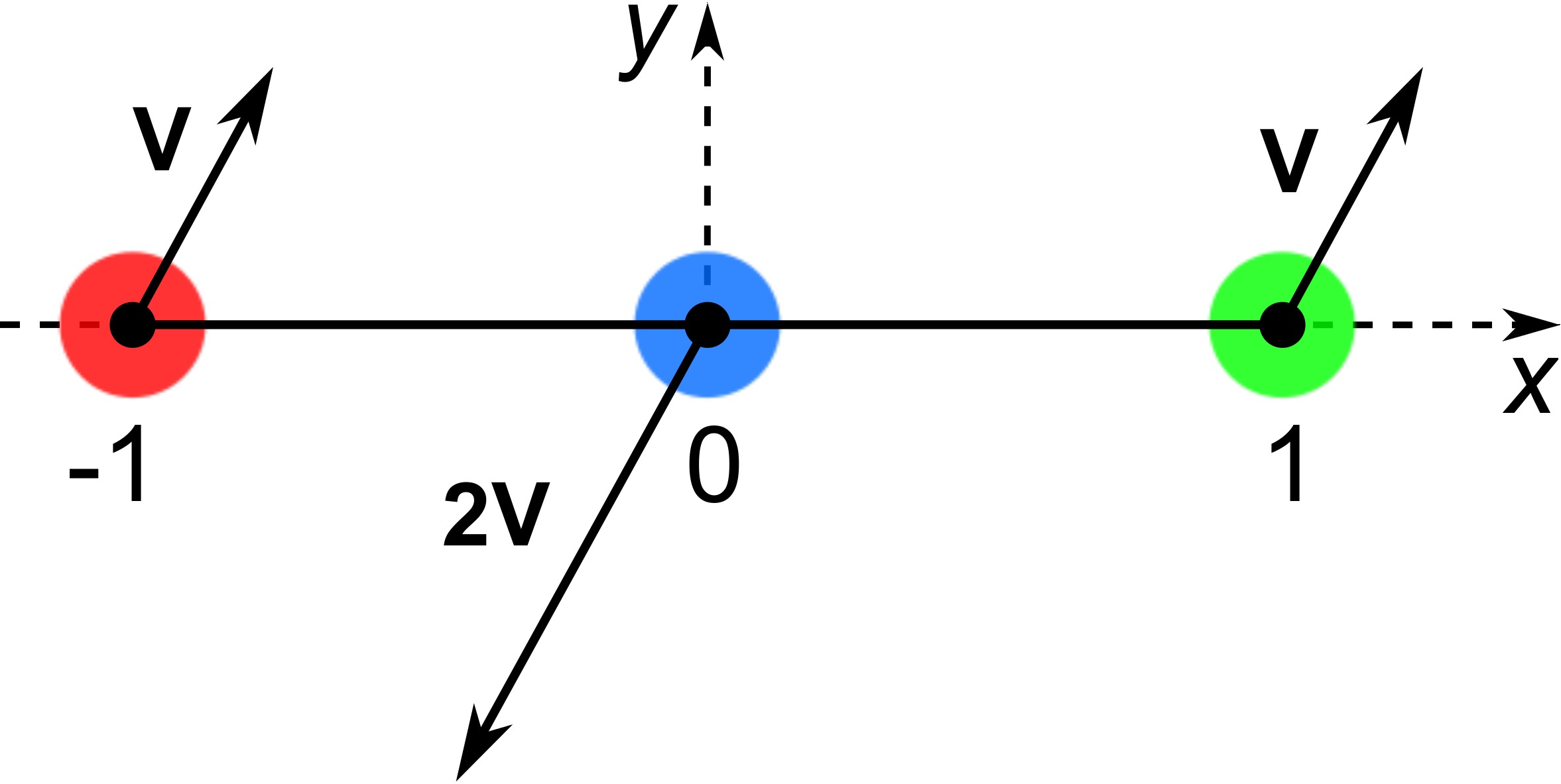
- Početni uslovi su:
- simetrična konfiguracija (Ojlerova tačka)
- paralelne brzine koje su u sumi nula i formiraju L=0
- dva parametra: $v_x$ i $v_y$ komponente $v$
- Koristimo Runge-Kutta-Fehlberg metod (RKF45): ukupna akumulirana greška $\sim 10^{-12}$
Strategija pretrage
- Tražimo minimum funkcije povratka:
\[d({\bf X}_{0},T_0) = min_{t\leq T_0}|{\bf X}(t) - {\bf X}(0)|, \] za fiksirano vreme $T_0$.
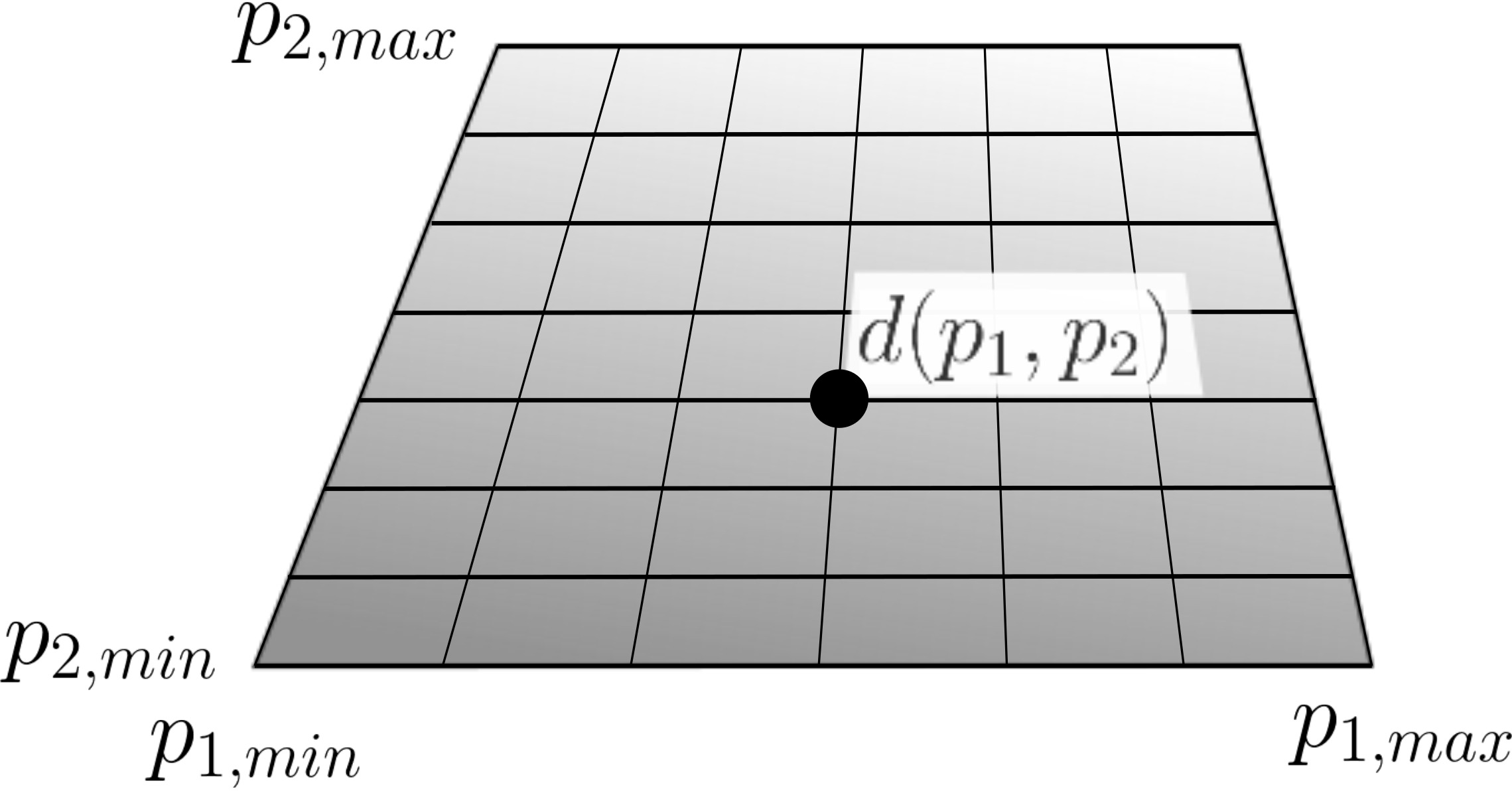
- Nakon lociranja regija minimuma, spuštamo se duž gradijenta kako bi se minimum odredio preciznije.
LOVIŠTE
- Fokus pretrage je na dvodimenzionalnom prozoru:
\[\dot x_1(0) \in (0,1), \dot y_1(0) \in (0,1)\]
- Jednačine kretanja su integraljene do:
\[T_0=100\]
- na rešetci dimenzija $1000 \times 1000$
[Šuvakov and Dmitrašinović, PRL 110, 114301 (2013)]
REŠENJA
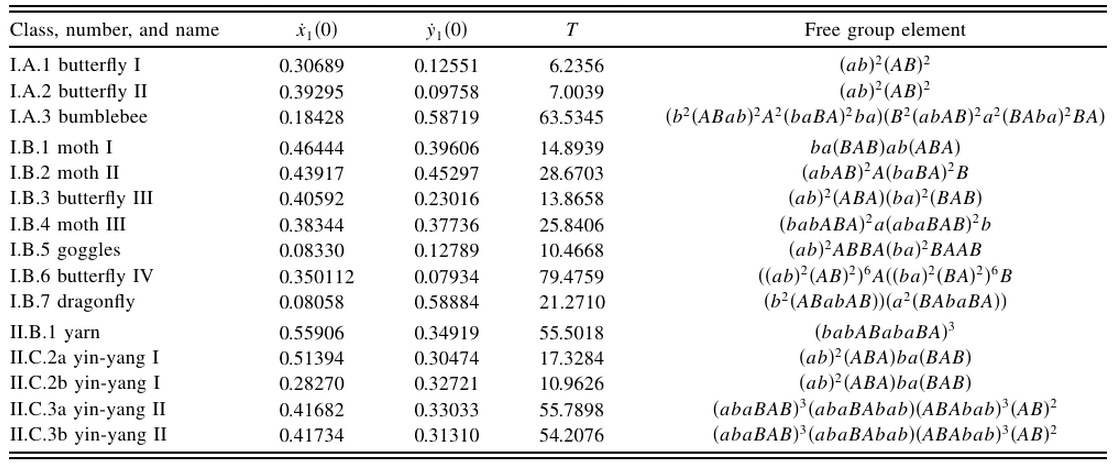
Klase rešenja
- Solutions can be classified according to their symmetries - geometrical
- I) two separate reflections w.r.t. two distinct axes (equator and zeroth meridian)
- II) one point reflection - joint reflections w.r.t. both axes
- Algebraic symmetries
- A) symmetric under $a \leftrightarrow A$ and $b \leftrightarrow B$;
- B) symmetric under $a \leftrightarrow b$ and $A \leftrightarrow B$
- C) no symmetry
GALERIJA REŠENJA
http://suki.ipb.ac.rs/3body/

http://orbitopedia.org
(u pripremi)
LEPTIR I
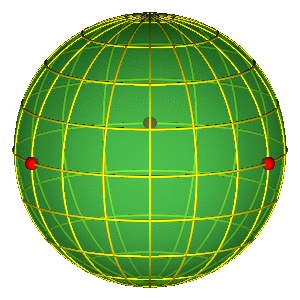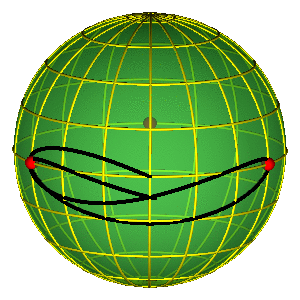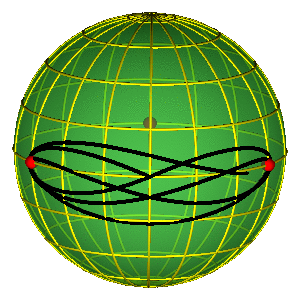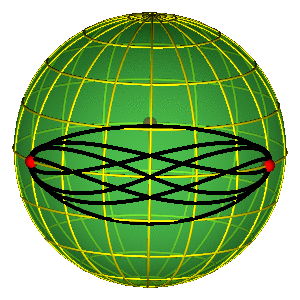
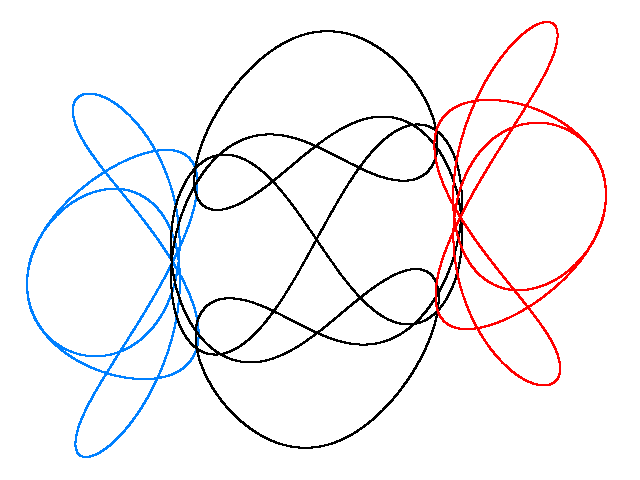
MOLJAC I
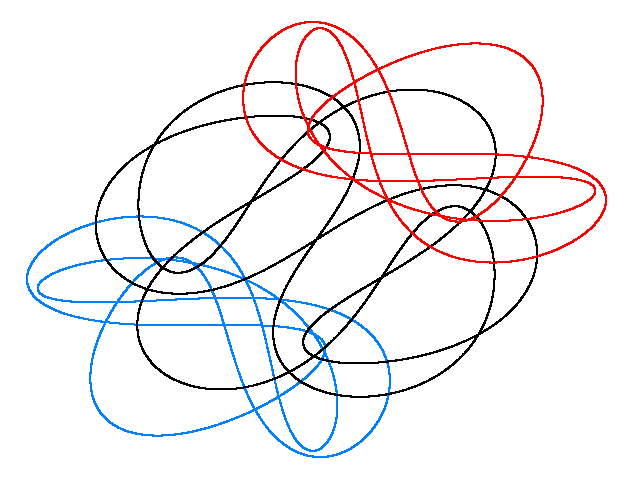
VILIN KONJIC

CVIKE
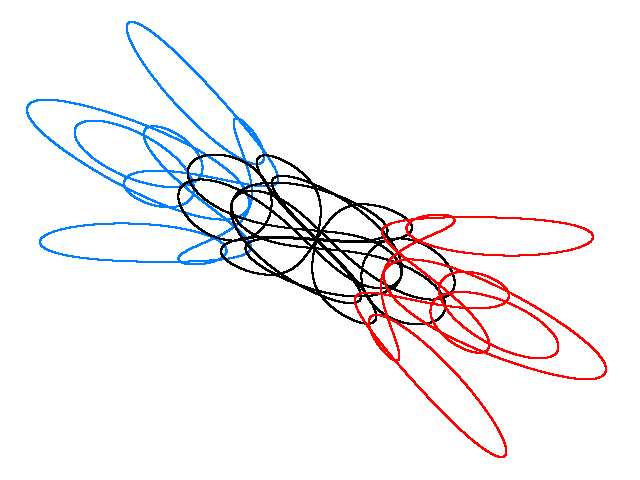
JIN-JANG I
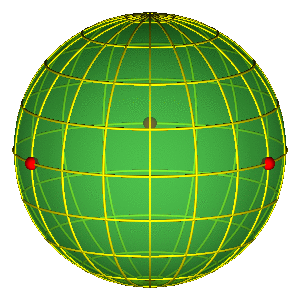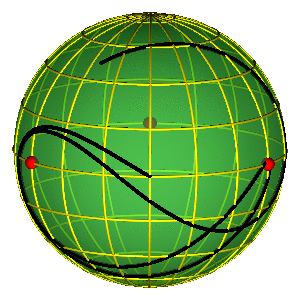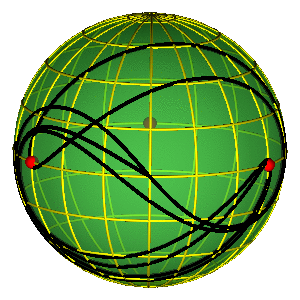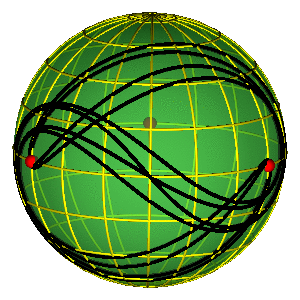
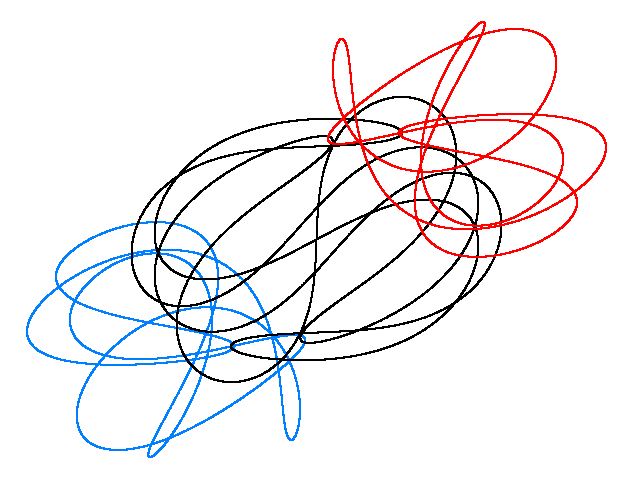
LEPTIR IV

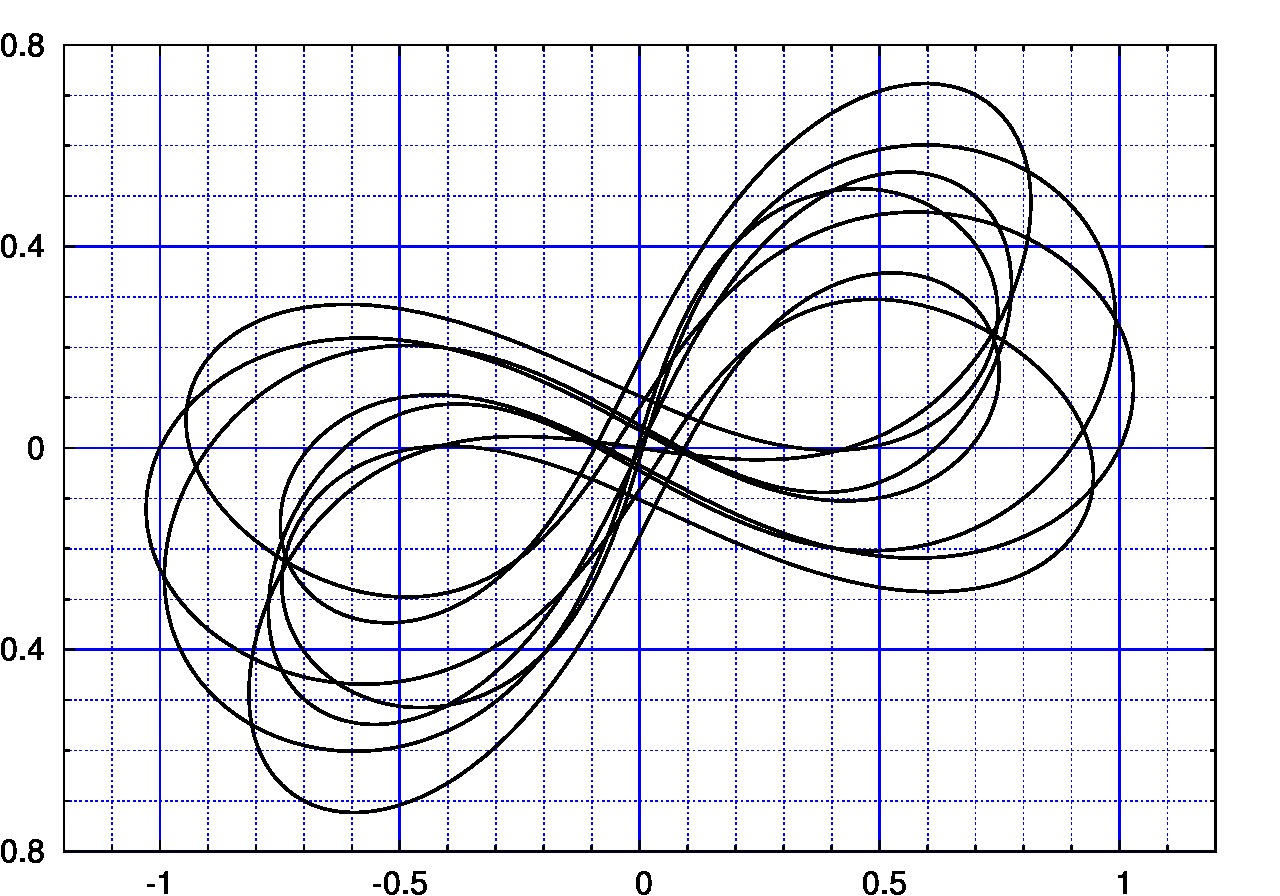
NOVA REŠENJA
- Fokus pretrage je na prozoru oko početnih uslova za osmicu:
$\dot x_1(0) \in (0.20,0.46)$, $\dot y_1(0) \in (0.51,0.56)$ - Jednačine kretanja su integraljene do $T_0=100$
- na rešetci dimenzija $130 \times 1000$
NEW CHOREOGRAPHY
ZAKLJUČAK, ŠTA DALJE?
- Urađeno sledeće:
- Nađeno 13 (+11) klasa rešenja
- Koristili smo topološki klasifikacioni metod (prvi put)
- Trenutno radimo na:
- Provera stabilnosti (M. Shibayama)
- Potraga za satelitima B-H-H rešenja (M. Janković)
- Gravitacioni talasi (A. Hudomal)
- Planovi za dalje:
- Proširivanje na različite mase i ugaone momente - ovo možda stabilizuje nestabilne orbite
- Uključiti relativnost
- Dublja pitanja: Koja rešenja postoje i zašto? Univerzalnosti?
PITANJA ?

http://suki.ipb.ac.rs/talks/pmfunis2014/