NEWTONIAN THREE-BODY PROBLEM
PERIODIC TRAJECTORIES AND TOPOLOGICAL CLASSIFICATION
Veljko Dmitrašinović ,Milovan Šuvakov
Laboratory for gaseous electronics
Center for non-equilibrium processes
Institute of physics Belgrad

Seminar at Beihang University, Beijing, 8th May 2013.
Transition Styles
You can select from different transitions, like:
Cube -
Page -
Concave -
Zoom -
Linear -
Fade -
None -
Default
Themes
Reveal.js comes with a few themes built in:
Sky -
Beige -
Simple -
Serif -
Night -
Default
* Theme demos are loaded after the presentation which leads to flicker. In production you should load your theme in the <head> using a <link>.
My collaborators Pavle and Milovan Šuvakov - The engines driving this project

Talk based on a recent paper:

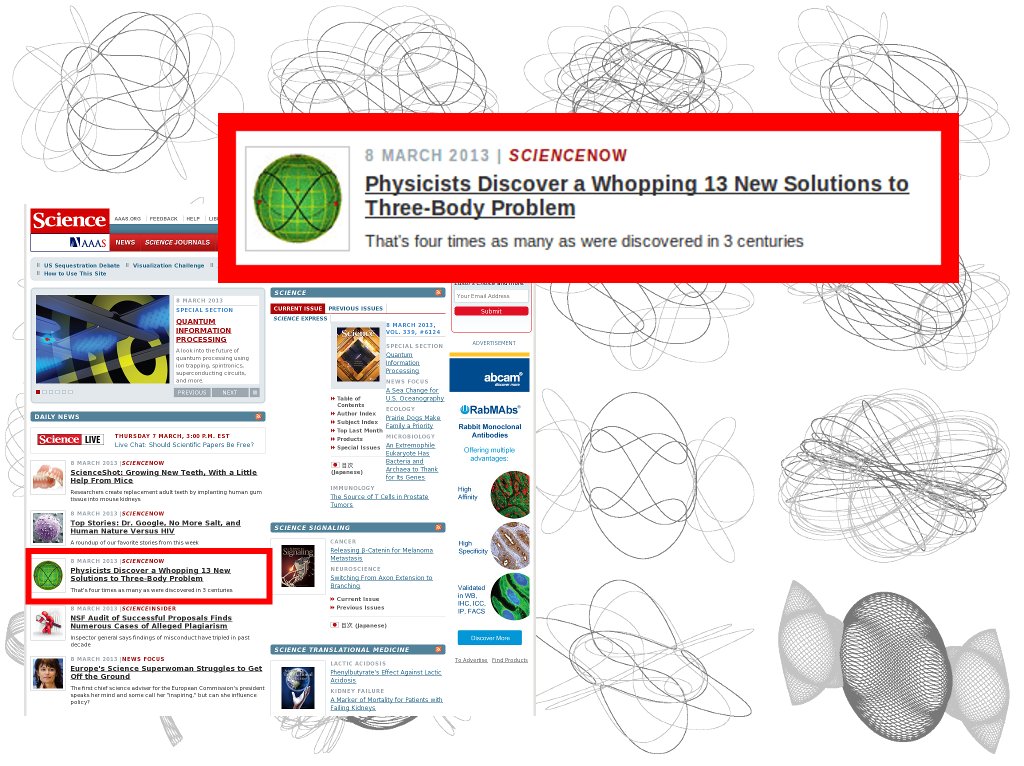
OUTLINE
- MOTIVATION: a personal message to students
- PROBLEM DEFINITION: review of the two-body problem
- KNOWN ORBITS: classical and more recent
- CLASSIFICATION OF ORBITS: braids, shape sphere
- HUNT FOR NEW SOLUTIONS
- CONCLUSIONS, OUTLOOK, OPEN QUESTIONS
[www.phdcomics.com]
PERSONAL MOTIVATION
- A MESSAGE TO STUDENTS:
WHY (NOT) WORK ON AGE-OLD PROBLEMS? - IMPORTANCE OF NEW METHODS:
SYNERGY OF ANALYTIC AND NUMERICAL WORK
MOTIVATION
- Confining three-quark potentials: the Y- and $\Delta$ string
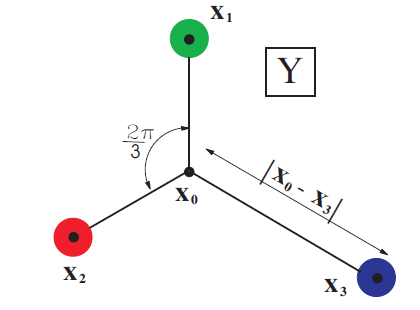
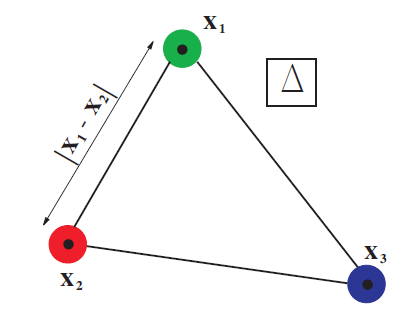
[V. Dmitrašinović, T. Sato, M. Šuvakov, Eur Phys J C 62 383 (2009)]
[V. Dmitrašinović, T. Sato, M. Šuvakov, Phys Rev D 80 054501 (2009)]
- Classical mechanical variant of the same problem
[M. Šuvakov, V. Dmitrašinović Phys Rev E 83 056603 (2011)]
TWO-BODY PROBLEM
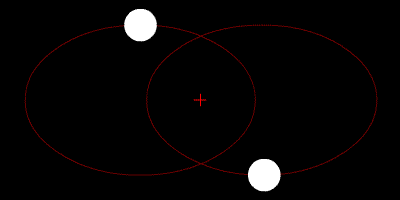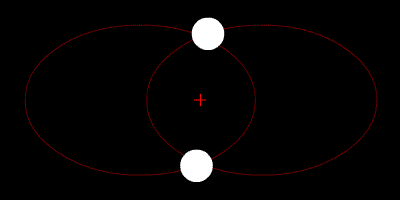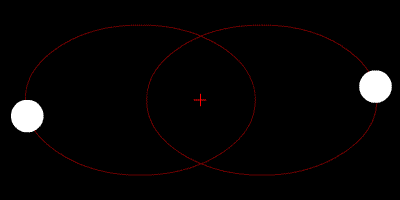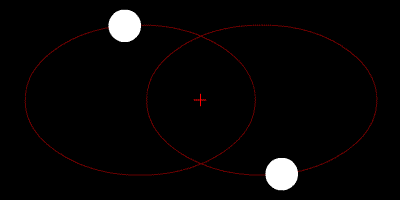
- Configuration space dimension: 2 x 2 = 4
- Phase space dimension: 2 x 4 = 8
- Conservation laws:
- energy: 1
- CM motion: 2 + 2
- angular momentum: 1
- Laplace-Runge-Lenz vector - 1
- Maximally super-integrable system (solutions?)
THREE-BODY PROBLEM

- Configuration space dimension: 3 x 2 = 6
- Phase space dimension: 2 x 4 = 12
- Conservation laws:
- energy: 1
- CM motion: 2 + 2
- angular momentum: 1
- remnant: 6 = 3 + 3
- No more [H. Bruns, Acta Math. 11, 25 (1887) ]
THREE-BODY PROBLEM
- Solutions can be:
- bounded / unbounded
- periodic / quasi-periodic / chaotic
- H. Poincare:
... what makes these (periodic) solutions so precious to us, is that they are, so to say, the only opening through which we can try to penetrate in a place which, up to now, was supposed to be inaccessible
KNOWN ORBITS
|
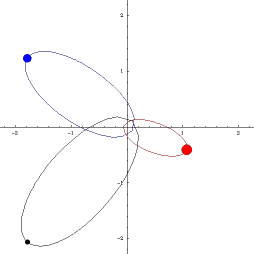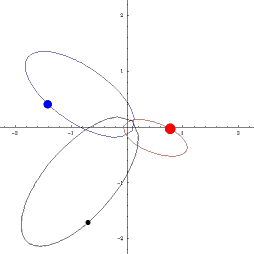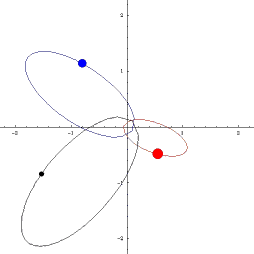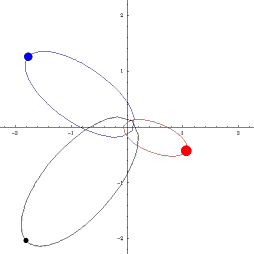 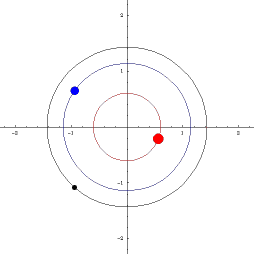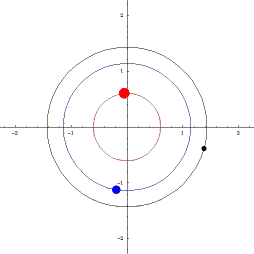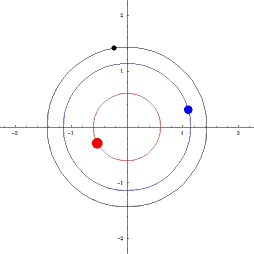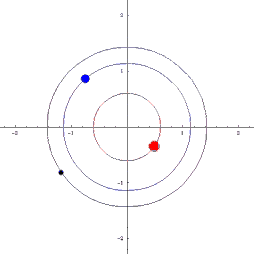
|
Classical orbits in astronomy:
|
 
|
MORE RECENT ORBITS
|
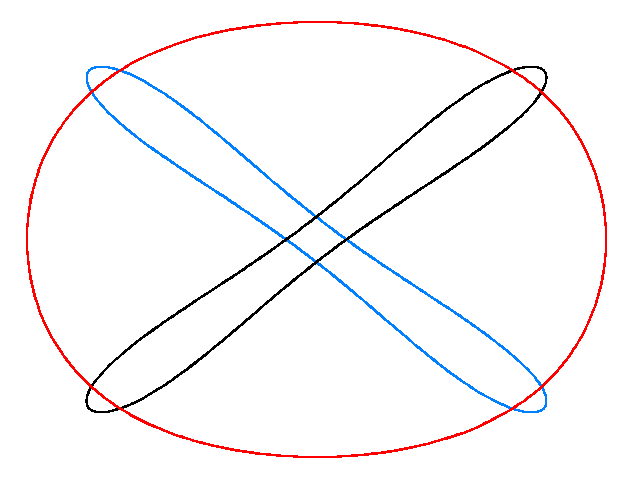 |
MOORE'S ORBITS
|
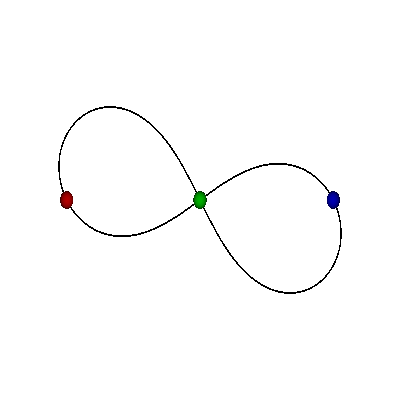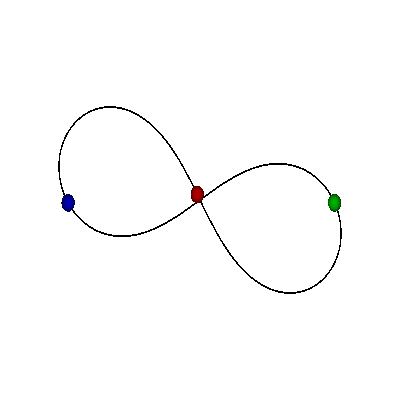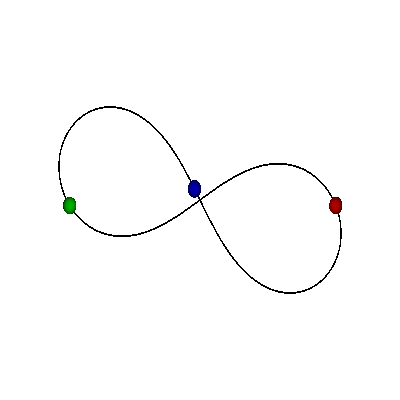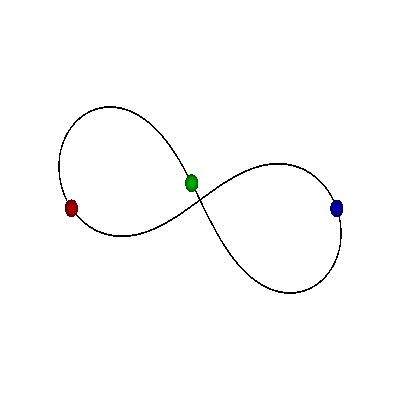
FIGURE-8
|
MOORE'S FIGURE-8
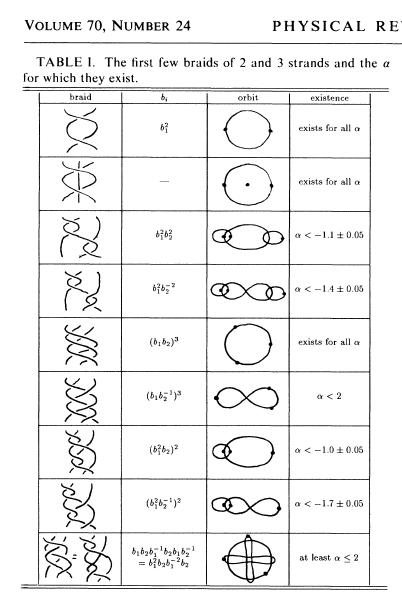
BRAIDS
JACOBI COORDINATES
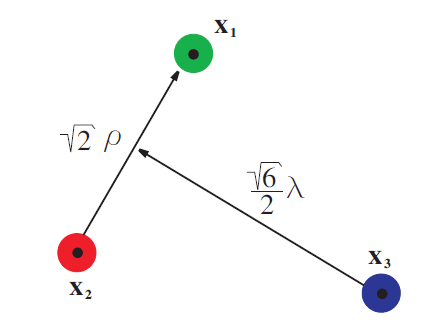 $$\rho = \frac{1}{\sqrt{2}} (\mathbf{x}_1-\mathbf{x}_2)$$
$$\lambda = \frac{1}{\sqrt{6}}
(\mathbf{x}_1+\mathbf{x}_2-2 \mathbf{x}_3)$$
Complicated representation of permutation symmetry!
$$\rho = \frac{1}{\sqrt{2}} (\mathbf{x}_1-\mathbf{x}_2)$$
$$\lambda = \frac{1}{\sqrt{6}}
(\mathbf{x}_1+\mathbf{x}_2-2 \mathbf{x}_3)$$
Complicated representation of permutation symmetry!
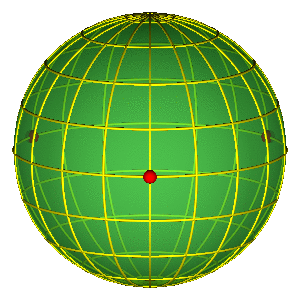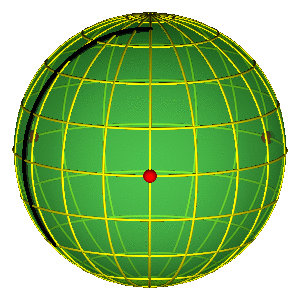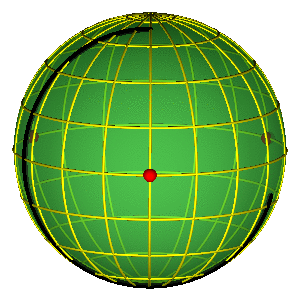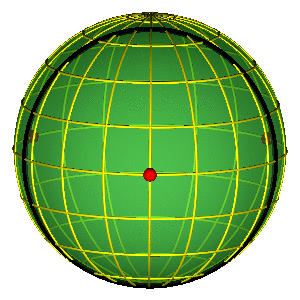
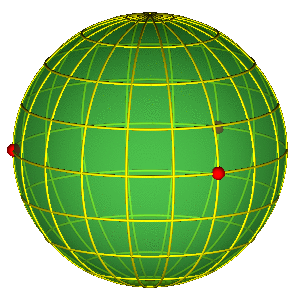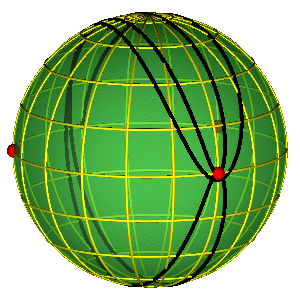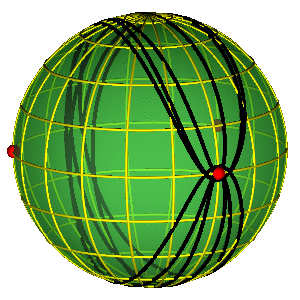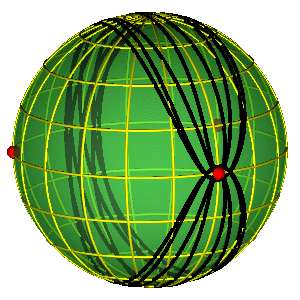
SHAPE SPHERE
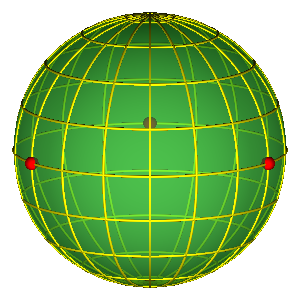 $$ \vec n = (n_x^{'},n_y^{'},n_z^{'}) = \left(\frac{2 {\vec \rho} \cdot {\vec \lambda}}{R^2}, \frac{\lambda^2 - \rho^2}{R^2}, \frac{2 ({\vec \rho} \times {\vec \lambda}) \cdot \vec e_z}{R^2} \right ) $$
$$R = \sqrt{\rho^{2} + \lambda^{2}}$$
Simple representation of permutation group!
$$ \vec n = (n_x^{'},n_y^{'},n_z^{'}) = \left(\frac{2 {\vec \rho} \cdot {\vec \lambda}}{R^2}, \frac{\lambda^2 - \rho^2}{R^2}, \frac{2 ({\vec \rho} \times {\vec \lambda}) \cdot \vec e_z}{R^2} \right ) $$
$$R = \sqrt{\rho^{2} + \lambda^{2}}$$
Simple representation of permutation group!
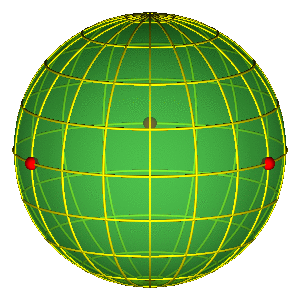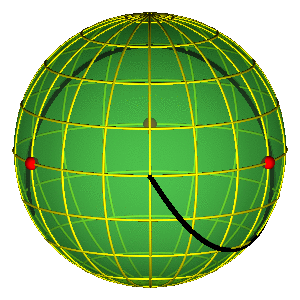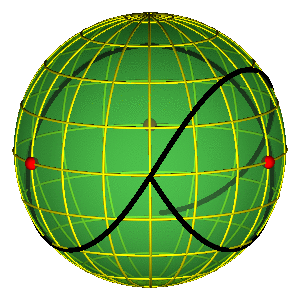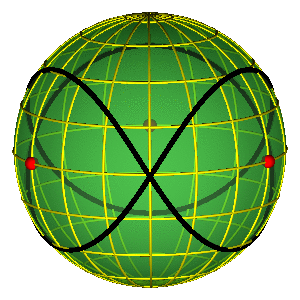
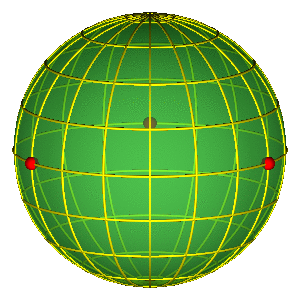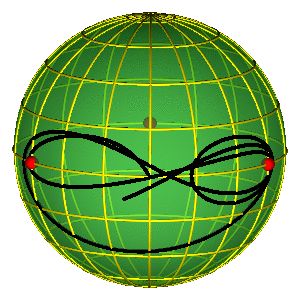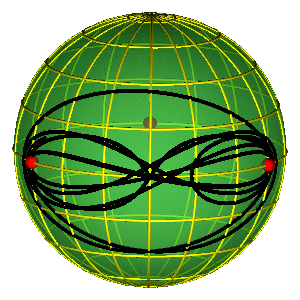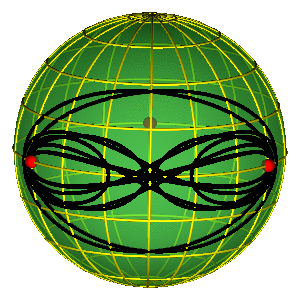
CLASSIFICATION OF ORBITS
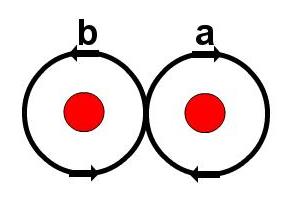
- Sphere without three points ~ plane w/o two
- Conjugation classes of a free group on two elements.
- For better legibility $A=a^{-1}$, $B=b^{-1}$.
- Broucke-Henon --- $a$
- Moore's figure eight --- $abAB$
BROUCKE-HENON & EIGHT
HUNT FOR NEW SOLUTIONS: ASSUMPTIONS
- Motion in a plane
- Equal masses
- Newtonian interaction ($-1/r$ potential)
- Under these conditions: permutation symmetry important, angular momentum is a "scalar", and the two-body collision configurations are the only singularities of the potential.
METHODS
- Runge-Kutta-Fehlberg method (RKF45)
- Accumulated error during one period $\sim 10^{-12}$
- Finding a solution is an optimisation problem
- Phase space: 6-dimensional
- Scaling: -1
- Collinear configuration: -1
- Middle point: -1
- $R'(0)=0$: -1
- Zero angular momentum $L=0$
SOLUTIONS
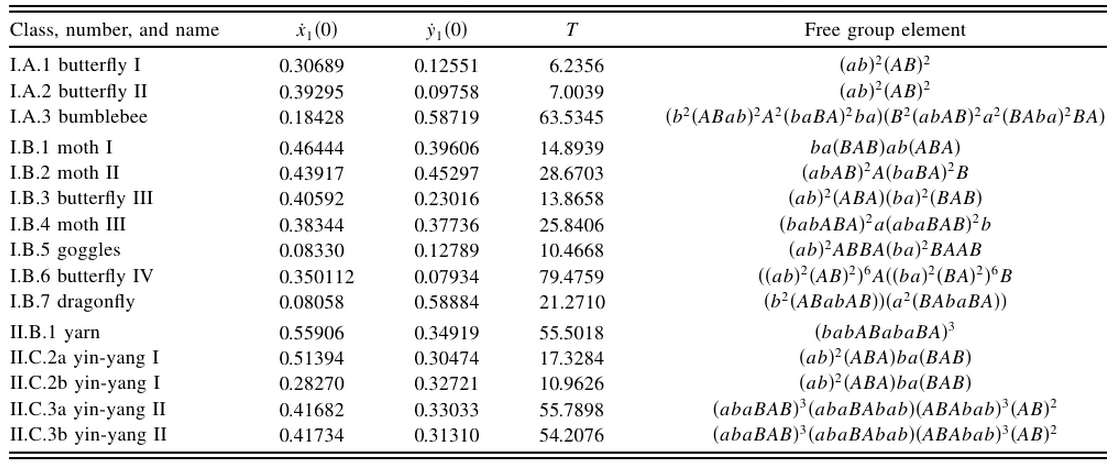
explain the classes!
BUTTERFLY I
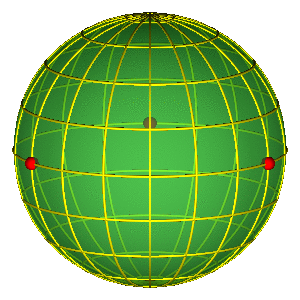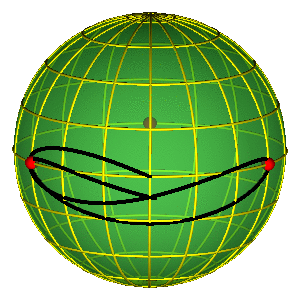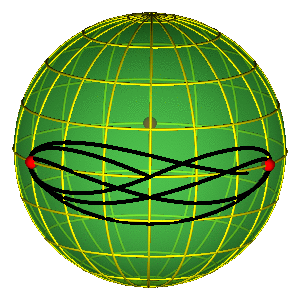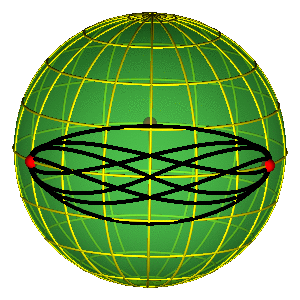
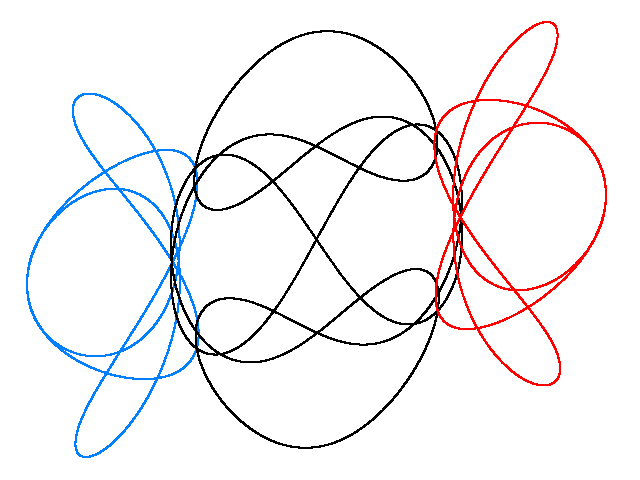
MOTH I
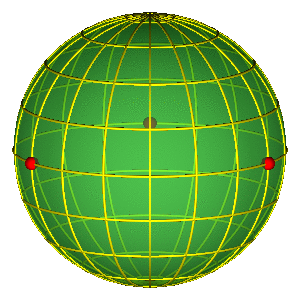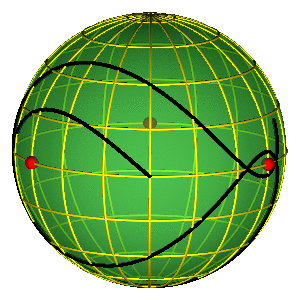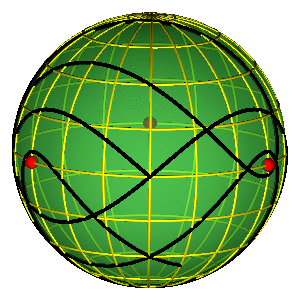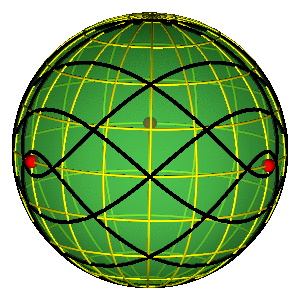
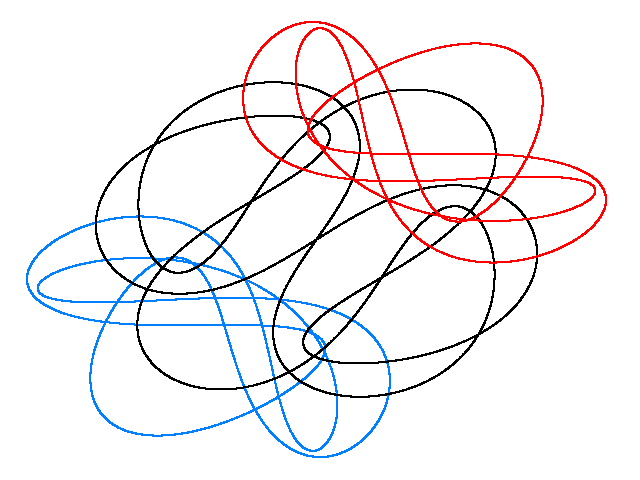
DRAGONFLY

GOGGLES
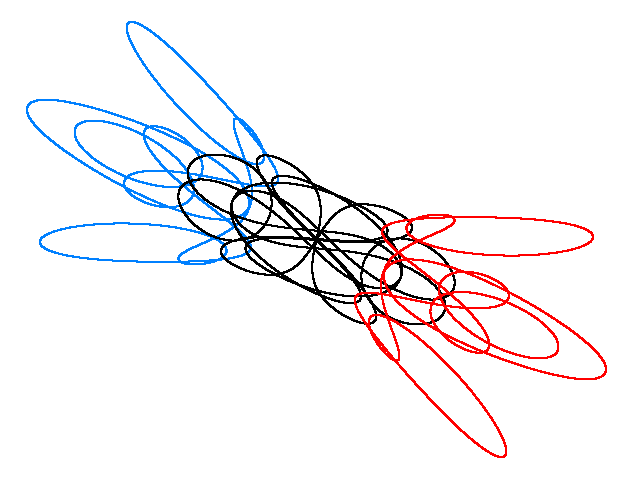
YIN-YANG I
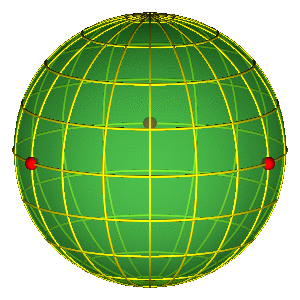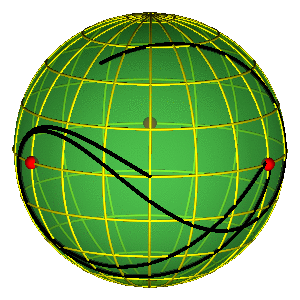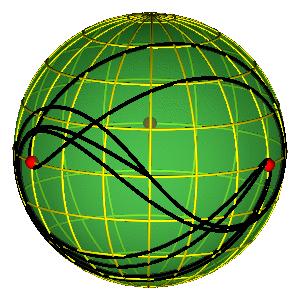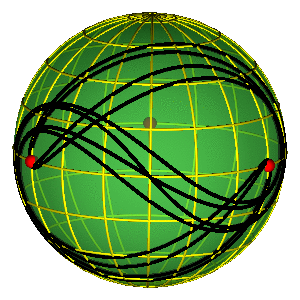
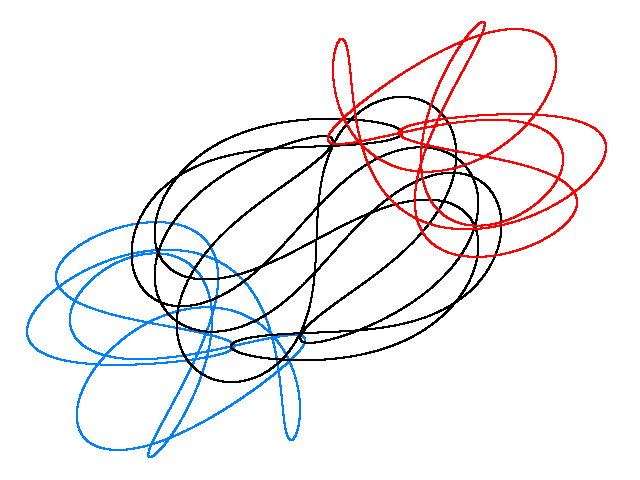
BUTTERFLY IV
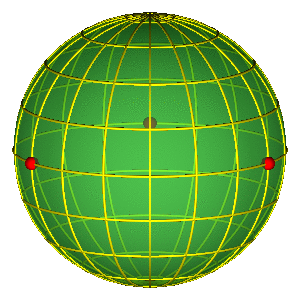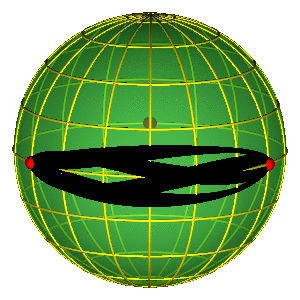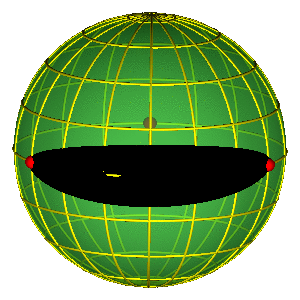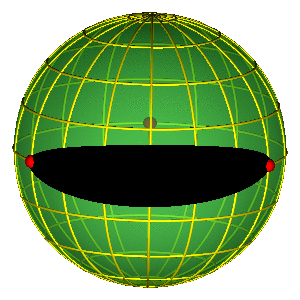

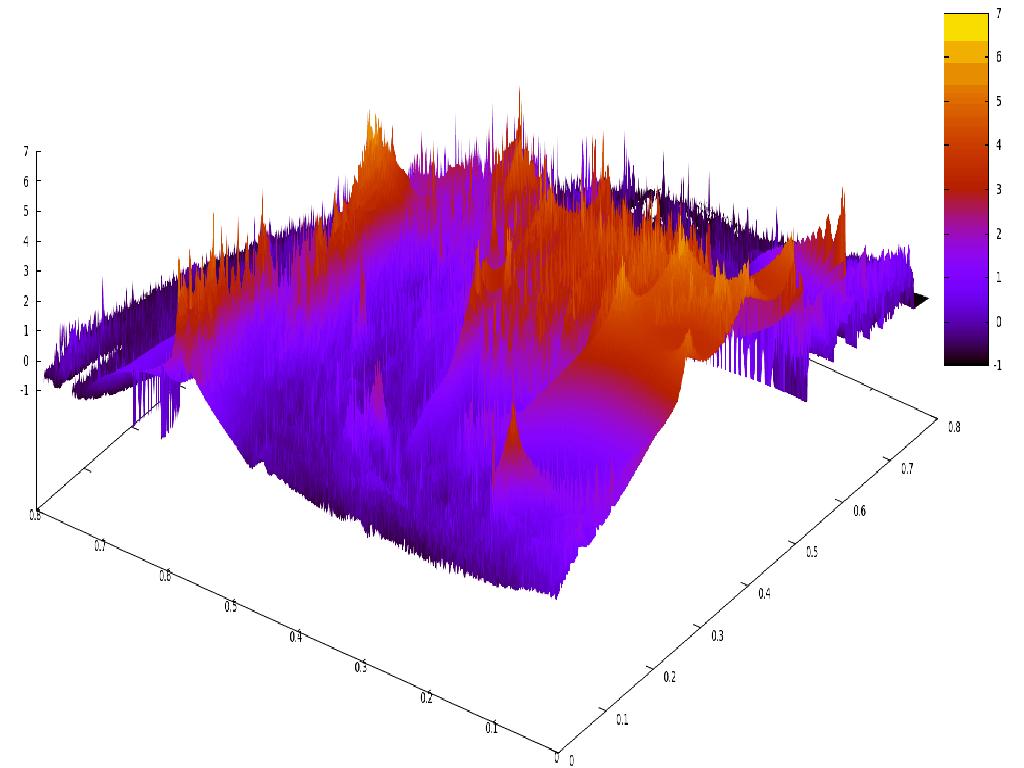
HUNTING GROUNDS
CONCLUSIONS, OUTLOOK
- We have:
- Found new solutions
- Used the topological classification method (first time)
- Future:
- Check of stability
- Extend to different masses and angular momenta
- Other systems (He atom with Coulomb interaction)
- Deeper questions: Why?
QUESTIONS ?

HUNTING GROUND - EARLY STEPS
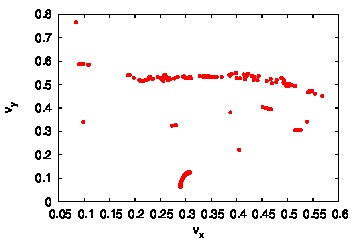
Similarities with Tasman's voyages?
Similarities with open-pit mining for diamonds?
 Kimberley "Big Hole" diamond mine in SA yielded 2,720 kilograms of diamonds; it was dug out by hand.
Kimberley "Big Hole" diamond mine in SA yielded 2,720 kilograms of diamonds; it was dug out by hand.
Open-pit mining for diamonds
 The Big Hole has a surface of 17 hectares and is 463 metres wide. It was excavated to a depth of 240 metres, but then partially infilled with debris reducing its depth to about 215 metres. It was hand-dug from 1871 to 1914 by up to 50,000 miners at a time.
The Big Hole has a surface of 17 hectares and is 463 metres wide. It was excavated to a depth of 240 metres, but then partially infilled with debris reducing its depth to about 215 metres. It was hand-dug from 1871 to 1914 by up to 50,000 miners at a time.
Deep mining for diamonds
 After 1914 the the kimberlite pipe was mined underground to a depth of 1,097 metres (machine excavated).
After 1914 the the kimberlite pipe was mined underground to a depth of 1,097 metres (machine excavated).
Modern open-pit mining for diamonds
 The Cullinan mine (SA) has yielded the world's two largest polished diamonds found thus far.
The Cullinan mine (SA) has yielded the world's two largest polished diamonds found thus far.
Results of modern open-pit mining

Deep mining for three-body orbits
 As we search for further orbits, their periods increase. It is like going deeper and deeper into a mine. Therefore, pretty soon we shall have to turn to machine-helped searches ("excavations") of periodic three-body orbits.
As we search for further orbits, their periods increase. It is like going deeper and deeper into a mine. Therefore, pretty soon we shall have to turn to machine-helped searches ("excavations") of periodic three-body orbits.